Skip to main content

METHODS TO MEASURE THE SPEED OF LIGHT

   From Einstein's famous equation E=mc2, we can measure the speed of light by putting the energy value and mass value in the equation. But that's just a theoretical process, practically it is not possible or it will not supply the correct value of speed of light. But in the field of practical physics, we have three methods proposed by HIPPOLYTE FIZEAU, LEON FOUCAULT and ALBERT A. MICHELSON. Now we will see how they measured the speed of light.

METHOD 1: FIZEAU METHOD

The first measurement of the speed of light from purely terrestrial experiments was reported by the French physicist HIPPOLYTE FIZEAU in 1849.
            Fizeau's experiment is illustrated below. A light source was focused through a beamsplitter onto an image plane where a spinning toothed wheel was located. The light passing between teeth of that wheel was then projected to a mirror at a distance of about 8 km, where it was collected and then reflected back to the point of origin. The rotational speed of the wheel was then increased until the returning light was blocked by the tooth on the wheel just adjacent to the space through which it had passed. Using this data, Fizeau was then able to calculate the speed of light. Limited by the precision of his measurements, Fizeau calculated the speed of light to be 315,000 km/s.


METHOD 2: FOUCAULT METHOD

In 1857, the French physicist Léon Foucault enhanced Fizeau method to measure the speed of light using a rotating mirror and a fixed mirror, as illustrated in the picture below.


Foucault's measurement is based on the following idea:

  • Light coming from the source hits a rotating mirror.
  • The rotating mirror reflects the light to a fixed mirror at a far distance (like 8,000 m).
  • Then fixed mirror the light back to rotating mirror.
  • This backward light will be bounded off the rotating mirror towards the light source with a small angle caused by the rotation. This angle can be used calculate the speed of light.

Using this idea, Foucault was able to measure the speed of light as 299,796,000 m/s. This is very close to today's definition of the speed of light: 299,792,458 m/s.



METHOD 3: MICHELSON METHOD

Michelson's method was devised in 1931 and is the most accurate out of all of the ones we have looked at yet.


          Light from an intense source S is incident on a polygon mirror M. Through further reflections this light is sent to a concave mirror M3. The geometry is set such that light from M3 is parallel. This parallel beam is allowed to travel a large distance after which it is converged at the focus of M4, and hits M5.

M5 reflects the beam back to M4, this time on its upper portion which again makes the beam parallel as it travels back to M3, after several reflections it returns to the polygon mirror and a telescope T is ready to receive the light from here.

Now if we rotate the polygon mirror such that while going the beam hits ab and while returning the polygon has rotated enough such that fg is now in the position of ab and reflects the light to T seamlessly. 

Therefore we must keep increasing the rotational speed till the beam becomes visible at T. If, N = no. of faces of the mirror, ω = angular speed at which light visible, D = total distance travelled by the light. Time taken by light to travel                         D=Δt=D/c    ,and angle rotates= Δθ=2π/Νa .Therefore,









These are the methods of calculating the speed of light.


CONCLUSION:-

This blog is written by TEAM ZEROSCIENCE. And we have collected data from these platforms----------

               1.@Vibingwithphysics(IG PAGE)
               2.https://en.wikipedia.org
               3.Stanford Encyclopedia of Philosophy

Catch us by clicking here ----- ZERO SCIENCE CONTACT.

                                                



d and

      

Labels:

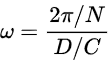
Comments

Post a Comment

Popular posts from this blog

Top 5 Amazing Classical Physics Experiments

Five Amazing Experiments That Changed the World of Classical Physics Physics might seem complicated, but it’s full of fascinating stories. Some of the most important discoveries in history started with simple questions, daring experiments, and brilliant minds that weren’t afraid to challenge the status quo. Let’s take a journey through five legendary experiments in classical physics that not only answered big questions but also opened the door to even bigger discoveries. Galileo’s Leaning Tower of Pisa Experiment: A Fall That Changed Everything Imagine this: It's the late 1500s , and the world still believes in Aristotle's ancient idea that heavy objects fall faster than light ones. But one man, Galileo Galilei, isn’t convinced. He decides to put this idea to the test in a way that would go down in history. Galileo climbs the Leaning Tower of Pisa , with two spheres of different masses in hand. Curious onlookers watch as he drops them at the same time. To everyone’s astonishm...
Post a Comment
Read more
Movie Review: Interstellar (2014) – A Journey Through Space, Time, and Humanity Christopher Nolan's Interstellar is not just another space adventure—it's an epic journey that pushes the boundaries of science fiction, blending intense human emotions with complex scientific concepts. Released in 2014, the film explores a future where Earth is slowly becoming uninhabitable, forcing humanity to look for survival beyond the stars. The plot follows Cooper (Matthew McConaughey), a former NASA pilot turned farmer, who is called upon to join a space mission to find a new habitable planet. As Earth faces ecological collapse, Cooper leaves behind his daughter, Murphy (Mackenzie Foy), and the rest of his family in hopes of saving humanity. What begins as a straightforward space exploration becomes an intricate story about time, love, sacrifice, and the sheer determination to survive. One of Interstellar's strengths is its attention to detail when it comes to scientific accuracy. With...
Post a Comment
Read more